AVE的全称是 Average Variance Extraction,翻译为平均方差提取量,
它是一个比率, 就是潜变量可以解释的方差占题目总方差的比率。
既然是比率, 它的取值就在(0, 1)之间, 这个值越大越好。
在结构方程(SEM)中,我们在做测量模型的效度分析的时候,
也就是验证性因子分析中,AVE是证明收敛效度的,平均提取方差值(AVE)是计算潜在变量之测量变量的变异数解释力,
若AVE越高,则表示构念有越高的信度与收敛效度。理想上标准值须大于0.5。
标准值0.5是由Fornell和Larcker在1981年提出的 ,
如果AVE低于0.5,但是CR高于0.6,也可以接受 (Fornell & Larcker, 1981) 。
我们在做结构方程的培训过程中, 很多同学会问如何理解AVE, 我们这里提供了公式推导和视频教程,
可以帮助里理解AVE。
AVE的计算公式

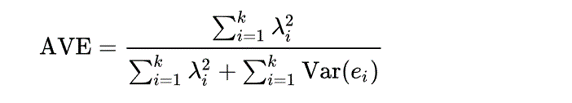
简单模型
上面的模型图可以转换为数学表达式:
$$ X_1 = \lambda_1 T + e_1 \\ X_2 = \lambda_2 T + e_2 \\ X_3 = \lambda_3 T + e_3 \\ ...\\ X_k = \lambda_k T + e_k \\ $$
方差的分解
对于两个独立的变量T和e, 方差具有如下性质:$X = T + e的方差为Var(X) = Var(T) + Var(e)$ ,
应用这个性质, 可以得到下面的方差公式:
$$ Var(X_1) = \lambda_1^2 Var(T) + Var(e_1)$ \\ Var(X_2) = \lambda_2^2 Var(T) + Var(e_2)$ \\ Var(X_3) = \lambda_3^2 Var(T) + Var(e_3)$ \\ ...\\ Var(X_k) = \lambda_k^2 Var(T) + Var(e_k)$ \\ $$
标准化数据方差为1
因为我们讨论的是标准化因子载荷λ, 因此公式里面看到的方差其实都是1,
所以可以简化为:
$$ 1 = \lambda_1^2 + Var(e_1)$ \\ 1 = \lambda_2^2 + Var(e_2)$ \\ 1 = \lambda_3^2 + Var(e_3)$ \\ ...\\ 1 = \lambda_k^2 + Var(e_k)$ \\ $$
化简AVE
$$ AVE = {\sum_{i=1}^k \lambda ^ 2 \over {\sum_{i=1}^k \lambda ^ 2 + \sum_{i=1}^k Var(e_i)} } \\ = {\sum_{i=1}^k \lambda ^ 2 \over {\sum_{i=1}^k [\lambda ^ 2 + Var(e_i)}] } \\ = {\sum_{i=1}^k \lambda ^ 2 \over k} $$
证明$\lambda ^ 2 = R^2$
在这篇文章中, 我们已经证明, 请跳转:公式推导证明相关系数等于决定系数R方
最终结论
$$ AVE = {\sum_{i=1}^k R_i ^ 2 \over k} $$